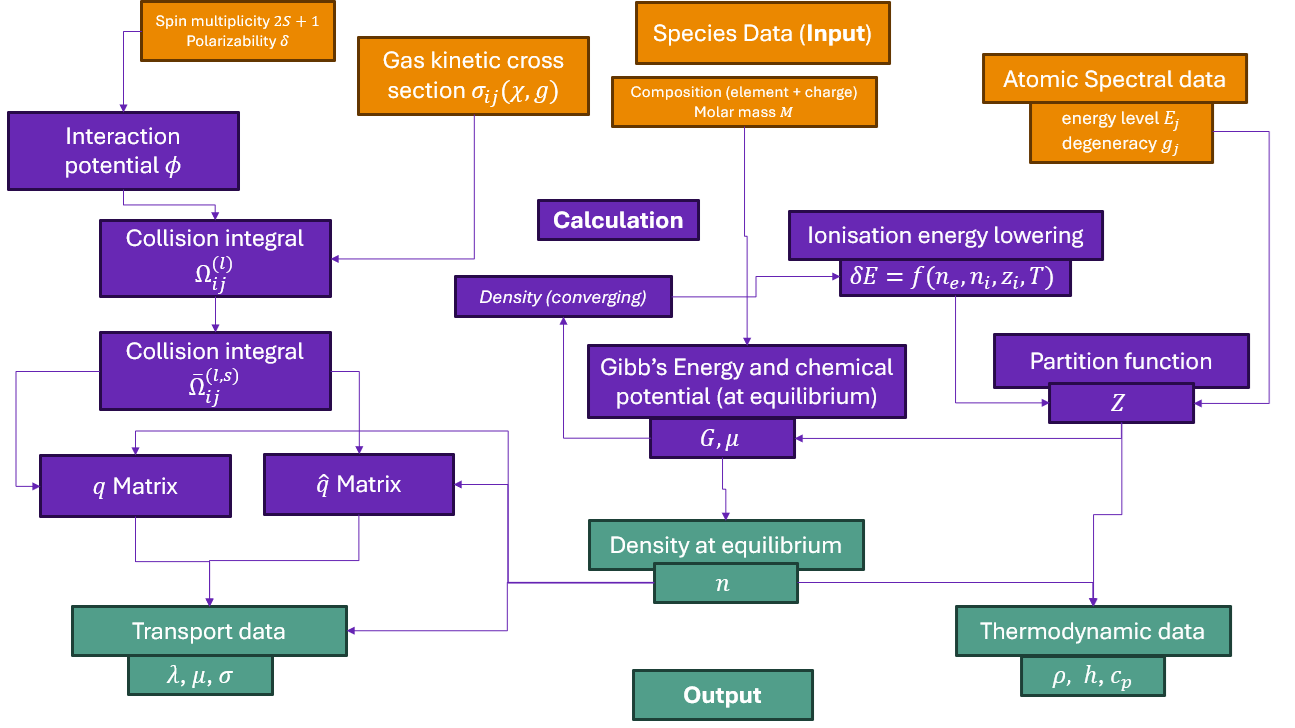
minplascalc.functions_radiation#
Radiation functions module.
Functions#
|
Compute the LTE total radiation emission coefficient of the plasma. |
Module Contents#
- minplascalc.functions_radiation.total_emission_coefficient(mix: minplascalc.mixture.LTE) float#
Compute the LTE total radiation emission coefficient of the plasma.
The total radiation emission coefficient is returned in W/m^3/sr.
- Parameters:
mix (
LTE) – Plasma mixture object containing species and temperature information.- Returns:
The total radiation emission coefficient in W/m^3/sr.
- Return type:
float
Notes
The explicit expression for the emission coefficient of a spectral line emitted by an atom or an ion as a function of temperature is given by equation 5 of chapter 20 of [Boulos2023], (and also at eq. 75 of chapter 7 of [Boulos2023]):
\[\varepsilon_L=\frac{1}{4 \pi} A_{u \ell}^r n_r \frac{g_{r u}}{Q_r} \exp \left(- \frac{ E_{r u} }{k_b T} \right) h \nu_{u \ell}\]where:
\(\varepsilon_L\) is the emission coefficient of the spectral line in \(\text{W.m}^{-3}.sr^{-1}\),
\(A_{u \ell}^r\) is the Einstein coefficient (or transition probability) for spontaneous emission in \(\text{s}^{-1}\),
\(n_r\) is the number density of the species, in \(\text{m}^{-3}\),
\(g_{r u}\) is the statistical weight of the upper state,
\(Q_r\) is the internal partition function of the species,
\(E_{r u}\) is the energy difference between the upper and lower states, in \(\text{J}\),
\(k_b\) is Boltzmann’s constant, in \(\text{J.K}^{-1}\),
\(T\) is the temperature, in \(\text{K}\),
\(h\) is Planck’s constant, in \(\text{J.s}\),
\(\nu_{u \ell}\) is the frequency of the transition, in \(\text{Hz}\),
\(\frac{1}{4 \pi}\) is the solid angle, in \(\text{sr}\).
Then, the total emission coefficient is calculated by summing the contributions of each emission line of each species in the mixture, using equation 6 of chapter 20 of [Boulos2023].
The number densities of the species are calculated by the mixture object, and the internal partition functions are calculated using the species object.
The formula used is derived from the Einstein coefficients for spontaneous emission and the Boltzmann distribution for the population of excited states.
The total emission coefficient is finally given by the following expression, expressing \(\nu_{u \ell}=\frac{c}{\lambda_{u \ell}}\):
\[\varepsilon = \frac{h c}{4 \pi} \cdot \sum_i \left( \frac{n_i A_{ij} }{Q_i \lambda_{ij}} \exp\left(-\frac{E_i}{k_B T}\right) \right)\]where:
\(\varepsilon\) is the total emission coefficient, in \(\text{W.m}^{-3}.sr^{-1}\),
\(h\) is Planck’s constant, in \(\text{J.s}\),
\(c\) is the speed of light, in \(\text{m.s}^{-1}\),
\(\pi\) is Pi,
\(n_i\) is the number density of species \(i\), in \(\text{m}^{-3}\),
\(A_{ij}\) is the Einstein coefficient for spontaneous emission, in \(\text{s}^{-1}\),
\(E_i\) is the energy of the lower state, in \(\text{J}\),
\(k_B\) is Boltzmann’s constant, in \(\text{J.K}^{-1}\),
\(T\) is the temperature, in \(\text{K}\),
\(Q_i\) is the internal partition function of species \(i\),
\(\lambda_{ij}\) is the wavelength of the transition, in \(\text{m}\).