Theory

Quick links

Tutorials on support utilities and species calculations

• Build a new monatomic species data entry.

• Build a new diatomic species data entry.

• Build a new polytomic species data entry.

• Calculate species partition functions.

Worked examples - oxygen plasma

• Calculate an equilibrium composition.

• Calculate density and heat capacity at equilibrium.

• Calculate transport and radiation properties at equilibrium.

Worked examples - silicon & carbon monoxide plasma

• Calculate an equilibrium composition.

• Calculate density and heat capacity at equilibrium.

• Calculate transport and radiation properties at equilibrium.

Target audience

Plasma technology researchers and professionals with a basic knowledge of the Python programming language.

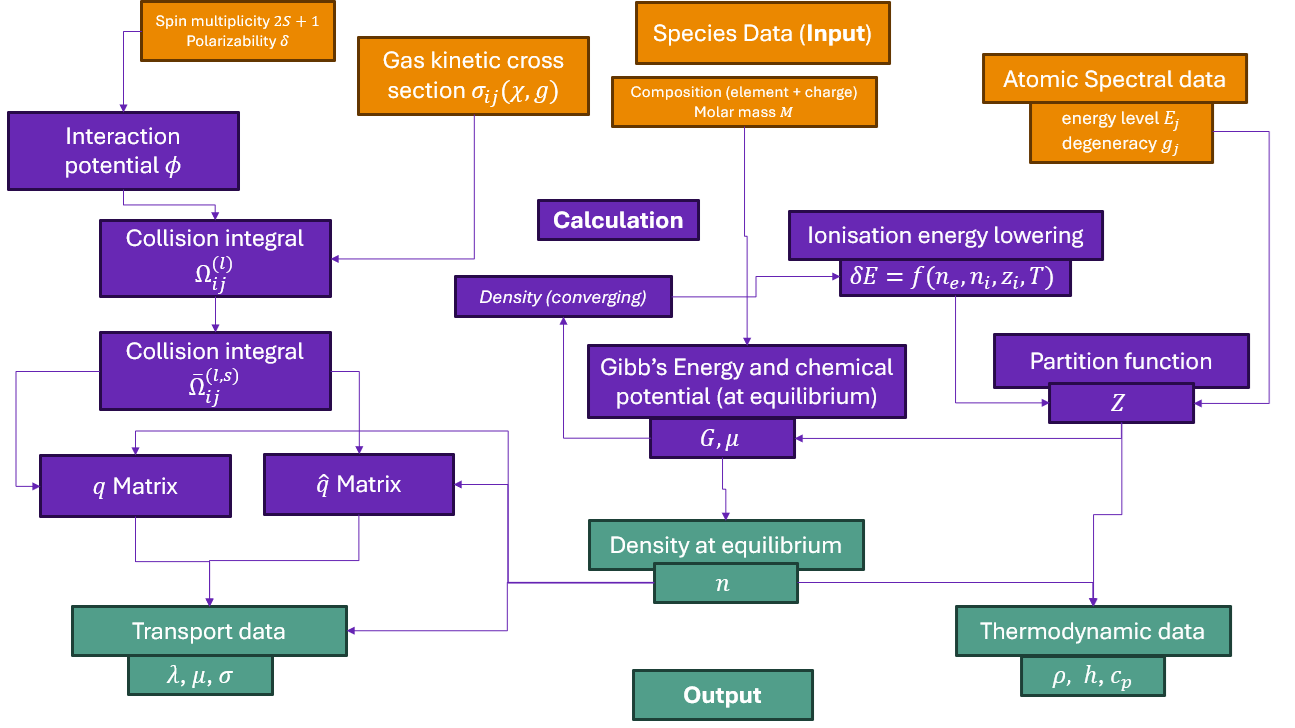
Module Description

Ionised gases or plasmas are used in many industrial applications such as arc welding, plasma spraying, and electric furnace metallurgy. Engineering plasmas typically operate at atmospheric pressures and temperatures of the order of 10⁴ K. Thermal plasmas of the sort considered here are assumed to be in local thermodynamic equilibirum (LTE), meaning that a single unique temperature can be used to describe them. A major advantage of the LTE approximation is that all thermophysical properties of an equilibrium mixture of an arbitrary number of plasma species can be expressed as (complicated) functions of temperature and pressure only - composition is implicit since it is uniquely determined by the state parameters.

Knowledge of these thermophysical properties is of great value to engineers working in plasma technology. Such information is useful for simple design calculations, and is necessary input data for computational fluid dynamics and magnetohydrodynamics models of plasma systems. The calculation of composition and thence the thermophysical properties of a thermal plasma given some fundamental information about the species present is a well-understood but mathematically and numerically complex process. It is prone to error if performed manually, hence the need for this tool.

Things you can calculate with minplascalc:

• Statistical mechanics partition functions for individual species using information about the energy levels and excited states

• Equilibrium plasma composition in terms of number densities of a specified mixture of species, using the principle of Gibbs free energy minimisation at a specified temperature and pressure

• Thermodynamic properties at LTE: density \(\rho\), (relative) enthalpy \(H\), and heat capacity \(C_P\).

• Transport properties at LTE: viscosity \(\mu\), electrical conductivity \(\sigma\), and thermal conductivity \(\kappa\).

• Radiation properties at LTE: total emission coeffient \(\epsilon_{tot}\).

Things you can’t calculate with minplascalc:

• Compositions or thermophysical properties of two-temperature or other non-equilibrium plasmas.

• Radiation absorption effects or effective emission coefficients.

Plasma theory

Partition functions

The starting point for thermal plasma calculations is generally the statistical mechanics partition functions for each of the species present. Users of minplascalc should not normally need to access these functions explicitly as they are incorporated directly into the composition and thermophysical property calculators, but they are exposed in the API in case the need to do so ever arises.

Recall that the partition function for a particular species is a description of the statistical properties of a collection of atoms or molecules of that species at thermodynamic equilibrium. Partition functions are normally presented as the sum of weighted state probabilities across the possible energy states of the system. In general at moderate plasma temperatures up to a few 10⁴ K, a species’ total partition function \(Q_{tot}\) can be written as the product of several unique partition functions arising from different quantum mechanical phenomena (assuming weak state coupling and no contribution from nuclear states):

\[Q_{tot} = Q_t Q_{int} = Q_t Q_e Q_v Q_r\]

Here, \(Q_t\) is the translational partition function due to the species’ ability to move around in space, \(Q_{int}\) is the internal partition function due to energy states internal to the particles of the species, \(Q_e\) is the electronic partition function due to different possible arrangements of the electron structure of the species, \(Q_v\) is the vibrational partition function due to the ability of the bonds in a polyatomic species to vibrate at different energy levels, and \(Q_r\) is the rotational partition function due to a species’ ability to rotate around its center of mass at different energy levels.

minplascalc distinguishes between four different types of species - monatomic (charged or uncharged single atoms), diatomic (charged or uncharged bonded pairs of atoms), polyatomic (charged or uncharged bonded groups of three or more atoms) and free electrons. The formulae used for the various partition functions for each are shown in the table below.

Partition Function	Monatomic	Diatomic	Polyatomic	Electron
\(Q_t\)	$${\left ( \frac{2 \pi m_s k_B T}{h^2}\right )}^{\frac{3}{2}}$$	$${\left ( \frac{2 \pi m_s k_B T}{h^2}\right )}^{\frac{3}{2}}$$	$${\left ( \frac{2 \pi m_s k_B T}{h^2}\right )}^{\frac{3}{2}}$$	$${\left ( \frac{2 \pi m_e k_B T}{h^2}\right )}^{\frac{3}{2}}$$
\(Q_e\)	$$\sum_i g_i \exp \left(-\frac{E_i}{k_B T}\right)$$	$$g_0$$	$$g_0$$	$$2$$
\(Q_v\)	$$1$$	$$\frac{\exp\left( -\frac{\omega_e}{2 k_B T} \right)}{1-\exp\left( -\frac{\omega_e}{k_B T} \right)}$$	$$\prod_i\frac{\exp\left( -\frac{\omega_{e,i}}{2 k_B T} \right)}{1-\exp\left( -\frac{\omega_{e,i}}{k_B T} \right)}$$	$$1$$
\(Q_r\)	$$1$$	$$\frac{k_B T}{\sigma_s B_r}$$	$$\frac{k_B T}{\sigma_s B_r},;or;\frac{\sqrt{\pi}}{\sigma_s} \sqrt{ \frac{(k_B T)^{3}}{A_r B_r C_r} }$$	$$1$$

Here $m_s$ and $m_e$ are the mass of one particle of the species concerned, \(k_B\) is Boltzmann’s constant, \(T\) is temperature, \(h\) is Planck’s constant, \(g_j\) and \(E_j\) are the quantum degeneracy and energy (in J) of electronic energy level j (with j = 0 being the ground state), and \(\omega_{e,i}\), \(\sigma_s\) and \(A_r,B_r,C_r\) are the vibrational, symmetry, and rotational constants respectively for a diatomic or polyatomic molecule.

minplascalc currently implements a complete electronic energy level set for single atoms and ions, but only the ground state level for diatomic molecules and ions. Since these species are generally present only at low temperatures where electronic excitation is limited compared to vibrational and rotational states, this approximation is reasonable.

Calculation of LTE compositions

Given temperature, pressure, and a set of species present in a plasma (and some information about the elemental composition of the mixture if more than one element is present), the number density of each species at thermodynamic equilibrium can be calculated using the principle of Gibbs free energy minimisation. This is an important intermediate step in calculating the thermopysical properties, and may also be useful in its own right if one is interested in the relative proportions of different species in complex plasmas. It is exposed to the user in the minplascalc API.

To start, recall the definition of Gibbs free energy:

$$G = G^0 + \sum_i \mu_i N_i$$

where \(G\) is the Gibbs free energy of a system, \(G^0\) is a reference value depending only on temperature and pressure, \(\mu_i\) is the chemical potential of species i, and \(N_i\) is the absolute number of particles of species i present. In terms of statistical mechanics properties, \(\mu_i\) can be represented as:

$$\mu_i = E_i^0 - k_B T \ln \left ( \frac{Q_{tot,i}V}{N_i} \right )$$

where \(Q\) is the partition function defined earlier, \(E_i^0\) is the reference energy of the species relative to its constituent uncharged atoms (for uncharged monatomic species and electrons \(E_i^0=0\), for uncharged polyatomic species it is the negative of the dissociation energy, and for charged species it is \(E_i^0\) of the species with one fewer charge number plus the lowered ionisation energy of that species), and \(V\) is the volume of the system. From the ideal gas law, we have:

$$V = \frac{k_B T \sum_i N_i}{P}$$

where $P$ is the specified pressure of the system.

A system at equilibrium is characterised by a minimum stationary point in \(G\), giving an independent equation for each species i which simplifies to:

$$\frac{\partial G}{\partial N_i} = \mu_i = 0$$

This set of equations must be solved subject to constraints supplied by the conservation of mass of each element present:

$$\sum_i v_{ik} N_i = \eta_k^0$$

where \(v_{ik}\) is the stoichiometric coefficient representing the number of atoms of element k present in species i, and \(\eta_k^0\) is the (fixed) total number of atoms of element k present in the system, obtained from user specifications. Together with this, one additional constraint is supplied by the requirement for electroneutrality of the plasma:

$$\sum_i z_i N_i = 0$$

In minplascalc, the previous three sets of equations are solved using an iterative Lagrange multiplier approach to obtain the set of \(N_i\) (and hence number density \(n_i = N_i / V\)) at LTE starting from an initial guess.

Ionisation energy lowering

In general the ionisation energy required to remove a single electron from a particle of a species is a constant for that particular species when considered in isolation. However, in a mixture of different species and free electrons, the ionisation energy is lowered by a small amount due to local electrostatic shielding effects. This affects both the calculation of the partition functions (the summation of electronic state contributions for monatomic species ignores states with energies above the lowered ionisation energy) and the calculation of equilibrium plasma compositions (the equilibrium relationships are defined using the reference energy levels for each species, which in turn depend on the lowered ionisation energies). Ionisation energy lowering is a complex problem in plasma physics, but there exist many approximate methods for quantifying this effect using the theory of Debye-shielded potentials. Provided the same method is used for all species, the calculation errors generally remain small. The ionisation energy lowering calculation is not exposed to the user in the minplascalc API, since it is only required internally for calculation of species partition functions and LTE compositions.

minplascalc uses the analytical solution of Stewart and Pyatt 1966 (see references in README). In this method, the ionisation energy lowering for each positively-charged species is calculated explicitly using:

$$\frac{\delta E_i}{k_B T} = \frac{\left [ \left (\frac{a_i}{l_D} \right )^3 + 1 \right ]^\frac{2}{3} -1}{2 \left( z^*+1 \right)}$$

where:

$$z^* = \left ( \frac{\sum z_j^2 n_j}{\sum z_j n_j} \right )_{j \neq e}, \quad a_i = \left ( \frac{3 z_i}{4 \pi n_e} \right )^\frac{1}{3}, \quad l_D = \left ( \frac{\epsilon_0 k_B T}{4 \pi e^2 \left ( z^* + 1 \right ) n_e} \right )^\frac{1}{2}$$

Here, \(\delta E_i\) is the amount the ionisation energy of species i is lowered by (in J), \(a_i\) is the ion-sphere radius of species i, \(l_D\) is the Debye sphere radius, \(z^*\) is the effective charge number in a plasma consisting of a mixture of species of different charges, \(z_j\) is the charge number of species j, \(n_j\) is the number density (particles per cubic meter) of species j, and \(e\) is the electron charge.

Calculation of thermodynamic properties

Plasma density

Given a plasma composition in terms of number densities \(n_i\), the mass density is a straightforward calculation:

$$\rho = \frac{1}{N_A} \sum_i n_i M_i$$

where \(M_i\) is the molar mass of species i in kg/mol, and \(N_A\) is Avogadro’s constant. The density calculation is exposed as a function call in the minplascalc API.

Plasma enthalpy

Calculation of the plasma enthalpy at a particular temperature, pressure, and species composition is performed using the statistical mechanics definition of internal energy:

$$U = -\sum_j \frac{1}{Q_j} \frac{\partial Q_j}{\partial \beta}$$

where \(U\) is the internal energy in J/particle for a particular species, \(Q_j\) are the various kinds of partition functions making up \(Q_{tot}\) for the species, and \(\beta=1/k_B T\). Formulae for \(U\) of various plasma species are thus readily produced using the expressions for \(Q_j\) given earlier.

Recall the thermodynamic definition of enthalpy:

$$H = U + p V$$

When multiple species are present, the relative reference energy \(E_i^0\) for each species must also be included. Application of the ideal gas law to the $pV$ term then gives:

$$H_i = U_i + E_i^0 + k_B T$$

where \(H_i\) is the enthalpy of species i in J/particle. Summing over all component species of a plasma and dividing by the density then gives the total enthalpy of the mixture in J/kg:

$$H = \frac{\sum_i n_i H_i}{\rho} = N_A \frac{\sum_i n_i H_i}{ \sum_i n_i M_i}$$

The enthalpy calculation is exposed to the user in the minplascalc API via a function call, however, it is important to note that the values obtained are relative to an arbitrary non-zero value for a given mixture.

Plasma heat capacity

A direct calculation of \(C_P\) given an arbitrary plasma composition is possible if some knowledge of the reaction paths between species is also supplied. Although any set of consistent reaction paths will give the same result, choosing one actual set of paths from the many possible options implies that it represents reality, and this is certainly open to some debate. In the spirit of keeping minplascalc focused on path-independent equilibrium plasma problems, the heat capacity calculation is instead performed by numerical derivative of the enthalpy around the temperature of interest:

\[C_{P,LTE} = \left( \frac{\partial H}{\partial T} \right)_p \approx \frac{H_{T+\Delta T,p} - H_{T-\Delta T,p}}{2 \Delta T}\]

Here, \(H_{T+\Delta T,p}\) and \(H_{T-\Delta T,p}\) are enthalpy calculations for the LTE plasma composition at fixed pressure, and temperatures slightly above and slightly below the target temperature $T$. This calculation is exposed to the user in the minplascalc API via a function call, and it is important to note that it only gives the heat capacity of LTE compositions.

Calculation of transport properties

Transport properties of plasmas are calculated using Chapman-Enskog theory developed from the principles of statistical mechanics. This is well described in references mentioned in the README, in particular those of Chapman & Cowling and Devoto.

Collision integrals

For calculation of transport properties of a mixture of particles in a dilute phase such as gas or plasma as a function of temperature and pressure, information is needed about both the composition of the mixture in terms of the species present, and the nature of collisions between pairs of particles. The former is obtained from free energy minimisation procedures described above, and the latter is described using quantities called collision integrals. Collision integrals are calculated as the effective geometric cross section between a given pair of particles, which is in general dependent on the physical nature of each particle as well as their closing velocity.

The collision integral in terms of integer moments \(l\) and \(s\) is derived from the gas-kinetic cross section \(\sigma_{ij}(\chi, g)\) by two successive integrations as follows:

$$\Omega_{ij}^{(l)} = 2 \pi \int_0^\pi \sigma_{ij}(\chi, g) \left(1 - \cos^l \chi \right) \sin \chi d\chi$$

\[\bar{\Omega}_{ij}^{(l,s)}= \frac{4(l+1)}{(s+1)!(2l + 1 - (-1)^l)} \int_0^\infty e^{-\gamma^2} \gamma^{2s+3} \Omega_{ij}^{(l)} (g) d\gamma\]

where \(\chi\) is the collision deflection angle, \(g\) is the closing velocity, and:

$$\gamma^2=\frac{m_r g^2}{2kT}, \quad m_r=\frac{m_i m_j}{m_i+m_j}$$

where \(m_r\) is the reduced mass of the colliding pair, and \(m_i\) are the particle masses.

In general collision integrals depend in complex ways on the interaction potential between the colliding pair, and may have both classical and quantum mechanical components. As these are difficult to calculate efficiently in closed forms, this has led to the development of many approximate or empirical expressions for various types of collisions. In minplascalc, we use the following:

	Neutral	Ion	Electron
Neutral	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{nn/in}\)	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{nn/in}, \theta_{tr}\)	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{e}\)
Ion	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{nn/in}, \theta_{tr}\)	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{c}\)	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{c}\)
Electron	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{e}\)	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{c}\)	\(\bar{\Omega}_{ij}^{(l,s)}=\theta_{c}\)

Elastic collision integrals \(\theta_{nn/in}\) for collisions between neutral heavy species or neutrals and ions are calculated using the empirical formulae of Laricchiuta et al. These were obtained by fitting to classical trajectory models using an extended and generalised Lennard-Jones type potential. The Laricchiuta expressions have the advantage of depending on only a few fundamental properties of the colliding species: their polarisability, the effective number of electrons contributing to polarisation, and the charge number in the case of neutral-ion collisions.

$$\ln \left( \frac{\theta_{nn/in}}{\pi x_0^2} \right) = \frac{A_1 + A_2 \ln \frac{k_B T}{\epsilon_0}}{1 + e^{-2 \xi_1} } + \frac{A_5 }{1 + e^{-2 \xi_2} }, \quad \xi_1 = \frac{\ln \frac{k_B T}{\epsilon_0}-A_3}{A_4}, \quad \xi_2 = \frac{\ln \frac{k_B T}{\epsilon_0}-A_6}{A_7}$$

In these expressions, \(x_0\) and \(\epsilon_0\) are parameters related to the Lennard-Jones potential used, and are defined in terms of the colliding species’ polarisabilities, effective electrons, and charge if applicable. \(A_i\) are polynomials in softness parameter \(\beta\), which is determined from the species’ polarisabilities. A full description of the model including tabulations of the polynomial coefficients for \((l,s)\) in the range 1 to 4 is available in Laricchiuta et al (see references in README).

The inelastic resonant charge transfer integral \(\theta_{tr}\) is only used for collisions between first ions and neutrals of the same species. It is obtained from approximate quantum mechanical calculations of an electron moving in the potential between two identical nuclei. In minplascalc we use the formula of Devoto 1967 (see references in README):

$$\theta_{tr} = B_1^2 - B_1 B_2 \bar{R} + \left( \frac{B_2 \bar{R}}{2}\right)^2 + \frac{B_2 \zeta_1}{2} ( B_2 \bar{R} - 2 B_1) + \frac{B_2^2}{4} \left (\frac{\pi^2}{6} - \zeta_2 + \zeta_1^2 \right) + \frac{B_2}{2} \left( B_2 (\bar{R} + \zeta_1) - 2 B_1 \right) \ln \frac{T}{M} + \left( \frac{B_2}{2} \ln \frac{T}{M} \right)^2$$

where:

$$\bar{R} = \ln (4R), \quad \zeta_1 = \sum_{n=1}^{s+1} \frac{1}{n}, \quad \zeta_2 = \sum_{n=1}^{s+1} \frac{1}{n^2}, \quad B_1 = \pi \frac{9.817 \times 10^{-9}}{I_e^{0.729}}, \quad B_2 = \pi \frac{4.783 \times 10^{-10}}{I_e^{0.657}}$$

\(R\) is the universal gas constant, \(M\) is the molar mass of the species, and \(I_e\) is its first ionisation energy in eV.

For collisions between charged particles, the collision integral \(\theta_c\) is calculated from classical trajectories of charges moving in a Coulombic potential. This is found to depend on a quantity called the Coulomb logarithm \(\ln \Lambda\). Empirical expressions have been developed for \(\ln \Lambda\) for three important classes of collisions: electron-electron, electron-ion, and ion-ion. For the temperature ranges of interest in thermal plasma calculations, and assuming equilibrium conditions, the NRL Plasma Formulary (see references in README) defines them as:

$$\ln \Lambda_{e-e} = 23.5 - \ln \left( n_e^{\frac{1}{2}} T^{-\frac{5}{4}} \right) - \left( 10^{-5} + \frac{(\ln T - 2)^2}{16} \right)^{\frac{1}{2}} $$

$$\ln \Lambda_{e-ion} = 23 - \ln \left( n_e^{\frac{1}{2}} z_i T^{-\frac{3}{2}} \right) $$

$$\ln \Lambda_{ion-ion} = 23 - \ln \left[ \frac{z_i z_j}{T} \left(\frac{n_i z_i^2 + n_j z_j^2}{T} \right)^{\frac{1}{2}} \right] $$

The appropriate expression for \(\ln \Lambda\) is then used to calculate the final collision integral for charged particles:

$$\theta_c = \frac{C_1 \pi}{s(s+1)} \left( \frac{z_i z_j e^2}{2 k_B T} \right)^2 \left[ \ln \Lambda - C_2 - 2 \bar{\gamma} + \sum_{n=1}^{s-1} \frac{1}{n} \right]$$

where \(\bar{\gamma}\) is the Euler gamma constant, and \(C_0\) and \(C_1\) take on different values with \(l\):

$$C_1^{l=1}=4, \quad C_1^{l=2}=12, \quad C_1^{l=3}=12, \quad C_1^{l=4}=16$$ $$C_2^{l=1}=\frac{1}{2}, \quad C_2^{l=2}=1, \quad C_2^{l=3}=\frac{7}{6}, \quad C_2^{l=4}=\frac{4}{3}$$

Calculation of the electron-neutral collision integral \(\theta_e\) from first principles is an extremely complex process and requires detailed knowledge of quantum mechanical properties of the target species. The complexity also increases rapidly as the atomic mass of the target increases and multiple excited states become relevant. In light of this, minplascalc opts for a simple empirical formulation which can be fitted to experimental or theoretical data to obtain an estimate of the collision integral for the neutral species of interest.

$$ \Omega_{ej}^{(l)} \approx D_1 + D_2 \left( \frac{m_r g}{\hbar} \right) ^{D_3} \exp \left( -D_4 \left( \frac{m_r g}{\hbar} \right)^2 \right) $$

In cases where insufficient data is available, a very crude hard sphere cross section approximation can be implemented by specifying only $D_1$ and setting the remaining \(D_i\) to zero. In all other cases, the \(D_i\) are fitted to momentum cross section curves obtained from literature. Performing the second collision integral integration step then yields:

$$\theta_e = D_1 + \frac{\Gamma(s+2+D_3/2) D_2 \tau^{D_3}}{\Gamma(s+2) \left( D_4 \tau^2 + 1\right) ^ {s+2+D_3/2}}, \quad \tau = \frac{\sqrt{2 m_r k_B T}}{\hbar}$$

\(q\) matrices

In the Chapman-Enskog formulation, the solutions to the Boltzmann transport equation are found to depend on quantities called bracket integrals. The bracket integrals are expanded using associated Laguerre polynomials, approximated to a specified number of terms indicated by integers \(m\) and \(p\). This produces expressions which are functions of the particle masses, concentrations, and collision integrals and are combined together in a matrix representing the set of possible binary collisions between all species in the plasma at a given level of approximation. For example, the matrix entries for the lowest approximation level are given by:

\[q_{ij}^{m=0,p=0} = 8 \sum_l \frac{n_l m_i^{\frac{1}{2}}}{(m_i + m_l^{\frac{1}{2}})} \bar{\Omega}_{il}^{(1,1)} \left[ n_i \left( \frac{m_l}{m_i} \right )^{\frac{1}{2}} (\delta_{ij}-\delta_{jl}) - n_j \frac{(m_l m_j)^{\frac{1}{2}}}{m_i} (1-\delta_{il}) \right]\]

Here, \(\delta_{ij}\) is the Kronecker delta. Full \(q\) matrix entry expressions for \(m\) and \(p\) from 0 to 3 are given in the appendix of Devoto 1966 (see references in README). Different expressions are used depending on whether the property being calculated is the diffusion coefficient or the viscosity - here we adopt Devoto’s convention and indicate them as \(q_{ij}^{mp}\) and \(\hat{q}_{ij}^{mp}\) respectively.

Normal and thermal diffusion coefficients

While not generally of direct interest in equilibrium calculations where diffusion kinetics do not play a role, the binary and thermal diffusion coefficients are an important intermediate calculation step for other properties of interest. Per Devoto 1966 (see references in README), we have:

$$ D_{ij} = \frac{\rho n_i}{2 n m_i} \left( \frac{2 k_B T}{m_i} \right)^{\frac{1}{2}} c_{i0}^{ji}$$

$$ D_i^T = \frac{n_i m_i}{2} \left( \frac{2 k_B T}{m_i} \right)^{\frac{1}{2}} a_{i0}$$

where the \(a\) and \(c\) values are determined from the solution of the linear systems:

$$ \sum_j \sum_{p=0}^M q_{ij}^{mp} c_{jp}^{hk} = 3 \pi^{\frac{1}{2}} (\delta_{ik} - \delta_{ih}) \delta_{m0}$$

$$ \sum_j \sum_{p=0}^M q_{ij}^{mp} a_{jp} = -\frac{15 \pi^{\frac{1}{2}} n_i}{2} \delta_{m1}$$

This calculation is not exposed directly to the user in the minplascalc API.

Plasma viscosity

Per Devoto 1966, viscosity \(\mu\) of a plasma mixture is given by:

$$\mu = \frac{k_B T}{2} \sum_j n_j b_{j0}$$

where values for \(b\) are obtained from the solution of the linear system:

\[\sum_j \sum_{p=0}^M \hat{q}_{ij}^{mp} b_{jp} = 5 n_i \left( \frac{2 \pi m_i}{k_B T} \right)^{\frac{1}{2}} \delta_{m0}\]

This calculation is exposed to the user in the minplascalc API via a function call, and it is important to note that it only gives the viscosity at LTE compositions.

Plasma electrical conductivity

Although conduction by ions does contribute to the overall electrical conductivity \(\sigma\) of a plasma mixture, the effect can generally be neglected due to the very large mass difference between electrons and ionic species. Using this approximation, we have from Devoto 1966:

$$\sigma = \frac{e^2 n}{\rho k_B T} \sum_{j \neq e} n_j m_j z_j D_{ej}$$

where \(D_{ej}\) are the binary diffusion coefficients of electrons relative to the heavy species.

This calculation is exposed to the user in the minplascalc API via a function call, and it is important to note that it only gives the electrical conductivity at LTE compositions.

Plasma thermal conductivity

The effective heat flux in equilibrium plasmas is a combination of various terms describing molecular transport, thermal diffusion, and chemical reaction. These can be presented in a variety of ways, but for minplascalc we choose the form in terms of the species flux gradient \(\mathbf{d_j}\) from Devoto 1966:

$$ \mathbf{q} = \sum_j \left( \frac{n^2 m_j}{\rho} \sum_i m_i H_i D_{ij} - \frac{n k_B T D_i^T}{n_j m_j} \right) \mathbf{d_j} - \left( \kappa’ + \sum_j \frac{H_j D_j^T}{T} \right) \nabla T $$

If we consider a system at constant pressure and with no external forces, we have:

$$ \mathbf{d_j} = \nabla x_j = \frac{dx_j}{dT} \nabla T $$

This allows us to express the total thermal conductivity \(\kappa\) as the pre-multiplication factor to \(\nabla T\) in the heat flux expression:

$$ \kappa = -\sum_j \left( \frac{n^2 m_j}{\rho} \sum_i m_i H_i D_{ij} - \frac{n k_B T D_i^T}{n_j m_j} \right) \frac{dx_j}{dT} + \kappa’ + \sum_j \frac{H_j D_j^T}{T} $$

The molecular thermal conductivity \(\kappa'\) is determined using the $a$ values obtained from the thermal diffusion coefficient calculation:

$$ \kappa’ = -\frac{5 k_B}{4} \sum_j n_j \left( \frac{2 k_B T}{m_j} \right)^{\frac{1}{2}} a_{j1} $$

As in the case of the plasma heat capacity it is possible to develop analytical expressions for the \(\frac{dx_j}{dT}\) term if some assumptions are made about reaction pathways, but this can be avoided simply by evaluating it numerically at the temperature of interest:

$$\frac{dx_j}{dT} \approx \frac{x_{j,T+\Delta T} - x_{j,T-\Delta T}}{2 \Delta T}$$

This calculation is exposed to the user in the minplascalc API via a function call, and it is important to note that it only gives the total thermal conductivity at LTE compositions.

Calculation of radiation properties

Thermal radiation in plasmas is an extensive field of study on its own, and covers a broad range of phenomena including line emission and absorption, continuum radiation, quantum mechanical effects, and many others. These are well documented in references such as Boulos et al (see references in README). Calculation of radiation behaviour becomes particularly complex when absorption effects are considered - at this stage, these are not included in minplascalc and only an estimate of the total emission coefficient can be calculated.

Total radiation emission coefficient

To a good first approximation in the temperature ranges of interest to thermal plasma applications, the total emission from a plasma mixture can be assumed to be purely line radiation from transitions between excited states in the constituent species. This can be calculated simply by integrating over wavelengths between 0 and \(\infty\) for each line in the emission spectrum for each species, and summing the results. Per Boulos et al, the formula for atomic species is:

$$ \epsilon_{tot} = \frac{\hbar c}{2} \sum_j \sum_{L} \frac{n_j g_{j,L} A_{L}^j}{Q_e^j \lambda_{j,L}} \exp \left( -\frac{E_{j,L}}{k_B T}\right )$$

Line wavelengths \(\lambda_{j,L}\), state degeneracies \(g_{j,L}\), transition probabilities \(A_L^j\), and energy levels \(E_{j,L}\) are readily available for most elements in atomic spectroscopy databases. Similar expressions can be used for molecular species, but these can often be omitted as they are only present at very low plasma temperatures where the total emission is relatively small and some inaccuracy can be tolerated.

The total emission coefficient calculation is exposed to the user in the minplascalc API via a function call, and it is important to note that it only gives the value at LTE compositions.